
Alan Turing i la seva gran aportació a la biologia matemàtica
-
- Home
-
- 1 of 1
Arran del centenari del naixement d’Alan Turing (1912-54) es van iniciar una sèrie de reconeixements a la figura d’aquest gran matemàtic britànic, fundador de la computació i precursor de la informàtica moderna, a més d’un reputat corredor d’ultramarató.
La pel·lícula Imitation games (2014, dirigida per Morten Tyldum) popularitzà la seva imatge. El llargmetratge mostra els trets principals de la seva intensa i curta vida amb especial èmfasi en la seva participació en el desxiframent dels codis nazis de comunicació de la màquina Enigma, que va ser crucial per al desenllaç de la guerra naval de l’Atlàntic.
Tanmateix, Alan Turing va fer moltes més aportacions en el camp de la matemàtica i del disseny de computadors. Un aspecte que vull destacar és una aportació a la biologia matemàtica desenvolupada els darrers anys de la seva vida, que encara avui en dia està ajudant a interpretar els fenòmens de desenvolupament i formació de patrons en els organismes vius. La carrera de Turing va acabar tràgicament amb el seu suïcidi a l’edat de 42 anys, dos anys després d’haver estat processat per homosexualitat i condemnat a un tractament hormonal castrador.
A finals del 2013, la reina Isabel II d’Anglaterra va promulgar un edicte que exonerava oficialment el gran matemàtic que va salvar moltes vides d'aliats i deixava anul·lats els càrrecs en contra seva. Una vegada més es fa palesa la incongruència del poder establert humà, que havia fet que uns prejudicis arruïnessin la vida d’una persona que al mateix temps havia estat un gran científic que havia innovat i havia aportat nous models de gran transcendència.
Permeteu-me aquí que us descrigui l’aportació d’Alan Turing en la modelització de patrons de morfogènesi (generació de la forma), mecanismes que es donen contínuament durant el desenvolupament i el creixement de plantes i animals a molts nivells.
El 14 d’agost de 1952 Turing va publicar l’article "The Chemical Basis of Morphogenesis" a la revista Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, vol. 237, issue 641, pàg. 37-72. L’article presenta un model matemàtic senzill que explica com es genera la forma en un embrió en creixement. El model pressuposa l’existència de molècules amb funció de morfògens (molècules que en funció de la seva concentració organitzen l’embrió) que es regulen mútuament i mitjançant dinàmiques de reacció i difusió i generen patrons complexos de regulació gènica diferencial que acaben produint patrons morfològics com la distribució radial dels tentacles d’una hidra o el patró de distribució de les fulles en la tija d’una planta. En la introducció de l’article el mateix Turing explica molt sincerament el propòsit del seu treball, que consisteix a generar un model matemàtic de l’embrió en creixement, i diu que el model és una simplificació i una idealització i, consegüentment, una falsificació!!!
Actualment, tanmateix, està àmpliament acceptat que la modelització de processos biològics ha esdevingut (i esdevé encara) un motor que ha empès els investigadors de la biologia del desenvolupament a testar noves hipòtesis i a generar així respostes que alhora han obert nous abordatges que ens permeten avançar en el coneixement de processos tan complexos com la generació de la forma i les proporcions.
Breument, el model de Turing, anomenat de reacció-difusió, considera dues molècules interrelacionades en un camp morfogenètic (territori embrionari en desenvolupament format per moltes cèl·lules equivalents): un activador i un repressor relacionats per interaccions, en les quals l’activador s’activa a si mateix alhora que activa el repressor i el repressor inhibeix l’activador i alhora s'autoinhibeix (fig. 1).
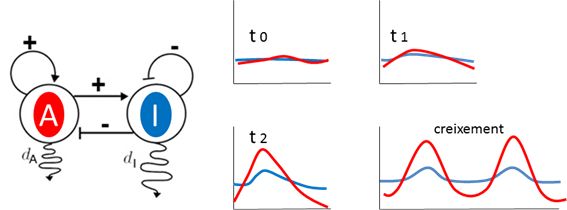
Figura 1. Model d’acció / reacció de Turing. A, activador, s’autoindueix +, i activa la síntesi de I, inhibidor. Alhora l’inhibidor reprimeix la seva pròpia síntesi - i la de l’activador. D’altra banda, la constant de difusió de l’activador dA és menor a la de l’inhibidor dI. A partir d’una distribució homogènia (t0), en condicions adequades, hi ha una autoorganització espontània (t1), en què, en certs punts, el nivell d’activador és superior al d’inhibidor (t2), cosa que genera estructures iterades en créixer, com són el patró de pigmentació o l'aparició de pèls en un insecte o de fulles en una planta
A més a més, té en compte els valors de difusió d’aquestes molècules dins un camp morfogenètic. El repressor té una constant de difusió més elevada que l’activador (fig.1). En el marc d’aquesta aparent falsificació, Turing va observar que les equacions que descriuen aquest model tenen solucions diferents: poden presentar distribucions homogènies si no es té en compte la difusió, però esdevenen inestables quan s’inclou el paràmetre de difusió. És a dir, petites desviacions de l’homogeneïtat s’incrementen i donen patrons diferents estocàstics. Un símil del patró de Turing, en reaccions oscil·lants, és l’observat en la sorra del desert: quan bufa el vent es formen petits monticles i valls, i a mesura que la cresta es fa més alta impedeix que es dipositin grans de sorra a les valls. Aquest exemple és equivalent al sistema activador / inhibidor que activa la cresta i inhibeix la vall (fig. 2).

Figura 2. A la part superior, sorra del desert, amb estructures ondulades, i pigmentació de melanina en una zebra, que correspondrien als patrons deduïts per Turing. A la part inferior, models de pigmentació del peix de les illes Seychelles Plectorhinchus vittatus i del nudibranqui Hypselodoris elegans, ambdues imatges cedides pel Dr. Kike Ballesteros del Centre d'Estudis Avançats de Blanes
El model de Turing s’ha emprat, des de la seva formulació, en moltes aplicacions. Per exemple, tenint en compte que el teòric activador incrementa l’acumulació de melanina (pigment animal de l’epidermis) a les cèl·lules es poden predir molts patrons de pigmentació complexos observats en el món animal, com ara la coloració en taques o franges de les serps, els felins o les zebres (fig.2). El patró quasi infinit de pigmentació dels organismes marins, que ja no depèn de la melanina, s’adaptaria igualment al model de Turing (fig. 2).
Hans Meinhardt, físic i professor emèrit del Max Planck Institute de Tübingen (Alemanya), ha desenvolupat al llarg de la seva carrera científica molts models biològics emprant les dades de la biologia molecular i models matemàtics basats en el model de Turing per explicar la formació del patró en teixits inicialment homogenis, mitjançant reaccions que combinen autoactivació local i inhibició de llarg abast. Així, ha explicat l’aparició d’estructures periòdiques com la distribució dels pèls en una mosca, de les fulles en una planta o dels porus en una fulla. També ha descrit models per explicar el procés de desenvolupament de les extremitats d’insectes i els fenòmens de restitució del patró en organismes adults, com és el cas de la regeneració d’organismes sencers en l’hidra (fig. 3) i en la planària. Tots aquests models aplicats en programes computacionals han sigut validats mitjançant experiments de biologia molecular. També ha explicat fenòmens universals com la iteració, la generació d’estructures repetides, la formació dels segments en insectes o dels somites en aus i mamífers.
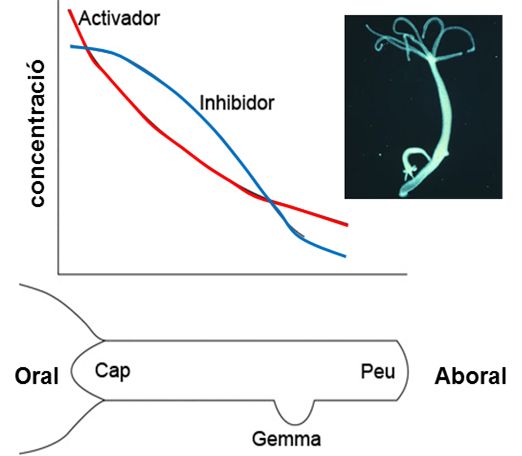
Figura 3. Model proposat per Meinhardt per explicar el manteniment de la polaritat de l’eix oral-aboral (cap-peu) a l’hidra. Segons aquest model, a la regió del cap hi ha la font de síntesi de l’activador, que en produir-se activaria l’inhibidor. La difusió més ràpida de l’inhibidor i, per tant, la seva major concentració respecte a l’activador, impediria la possibilitat de generar un nou cap en zones orals. En regions aborals s’inverteix l’equilibri i es pot produir un nou centre organitzador del cap que formarà una gemma lateral que permetrà formar una nova hidra.
Les aplicacions del model de Turing no tenen aturador. L’any 2014 es va emprar per explicar un model que ajuda a entendre la formació dels cinc dits a les nostres extremitats. El fet de tenir cinc dits ens permet agafar objectes i, per tant, explorar i manipular el nostre entorn tridimensional. Així, els cinc dits em permeten a mi escriure aquest article divulgatiu i a vosaltres clicar el ratolí per poder-lo llegir. A part de la utilitat d’aquestes mans i peus amb cinc dits i la seva complexitat a l’hora de desenvolupar-se, hi ha moltes preguntes al voltant de com es construeixen les diferents regions iterades de dit / espai interdigital. Tradicionalment, el model de la formació del patró dels dits es basava en la presència de gradients de morfògens que, en funció de la seva concentració, definien uns valors posicionals que eren interpretats per les cèl·lules. La integració de la biologia del desenvolupament en la modelització computacional basat en el model de Turing ha permès fer un salt qualitatiu i observar el procés amb nous paràmetres en què es té en compte la capacitat d’autoorganització del territori precursor dels dits per establir les periodicitats. A partir d’un territori homogeni, s’autoorganitzaria un patró de condensacions de cartílag que s’amplificaria seguint el model de reacció-difusió d’activador / inhibidor i formaria espontàniament el patró periòdic dels dits. Aquest patró seria diferent si són extremitats humanes, amb cinc dits, de cavall amb un de sol, de camell amb dos o del fòssil Acanthostega amb vuit.
Una conseqüència important d’aquests resultats ens porta a veure els processos complexos de formació del patró durant el desenvolupament com a resultat d’una expressió diferencial dels gens en un entorn que s’autoorganitza segons el model de reacció-difusió de Turing.
En resum, el model simplificat proposat per Turing fa més de 60 anys ens ajuda a millorar la comprensió de fenòmens molt complexos d’autoorganització imprescindibles per explicar el desenvolupament embrionari i la regeneració dels éssers vius.





