El nombre d’or i l’anomenada successió de Fibonacci

El matemàtic italià Leonardo Bonacci (1170-1240), conegut també com a Leonardo de Pisa per haver nascut en aquesta ciutat, va passar a la posteritat amb el sobrenom de Fibonacci, que prové de l'expressió llatina figlio di Bonacci (‘fill de Bonacci’).

Leonardo Bonacci

Fibonacci va difondre per occident els caràcters aràbics i va publicar el Liber abbaci, potser un dels millors textos d’àlgebra coneguts –escrit l’any 1202–. En aquest llibre exposa problemes algebraics aplicats a la resolució de problemes del comerç i plasma la importància del sistema de numeració hindú i aràbic.

D’aquesta obra només es conserva la segona edició –publicada el 1228– on a les pàgines 123 i 124 destaca un curiós problema relacionat amb el creixement d’una població de conills. En aquest problema apareix una seqüència numèrica que es coneix com a successió de Fibonacci i que té la particularitat d’estar estretament relacionada amb el nombre d’or.

Vegem detalladament l’esmentat problema.

L’enunciat parteix del fet que en un lloc tancat es diposita una parella de conills per observar quants descendents produeixen en el curs d’un any. La hipòtesi de treball planteja el següent model: el primer mes la parella no és fèrtil, i a partir del segon mes la parella en reprodueix una de nova.

Segons aquesta hipòtesi, si suposem que no es mor cap parella, al cap de set mesos passarem de tenir una parella a tenir-ne 13, tal com mostra la imatge:

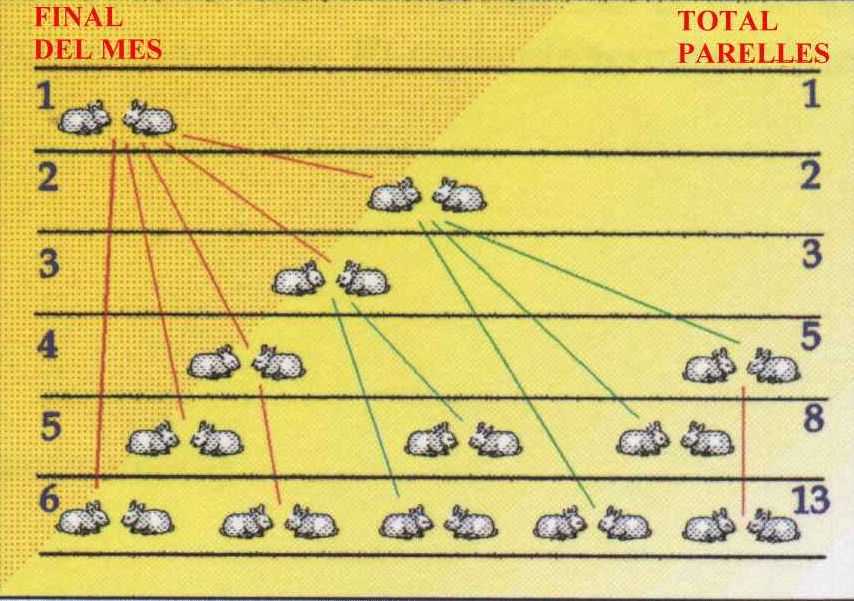
Tot seguit comptarem el nombre de parelles que hi ha al final de cada mes.

Primer mes: La inicial p₀ (total 1 parella).

Segon mes: La inicial p₀, perquè encara no és fèrtil (total 1 parella).

Tercer mes: Ja procrea; tenim una nova parella p₁ i la p₀ que ja teníem (total 2 parelles).

Quart mes: La p₁ encara no és fèrtil, p₀ en fa una altra, diguem-li p₂ (total 3 parelles).

Cinquè mes: La p₁ ja és fèrtil; tenim, doncs, la p₁ i els fills de p₁, que anomenarem p₃; la p₀ procrea, diguem-li p₄ (total 5 parelles).

La seqüència numèrica és: 1, 1, 2, 3, 5, 8, ..., que es coneix pel nom de successió de Fibonacci.

El lector pot observar que cada terme s’obté sumant els dos anteriors, és a dir:

1 + 1 = 2

1 + 2 = 3

2 + 3 = 5

3 + 5 = 8

...........

Què té de curiós la successió de Fibonacci? En síntesi, que si efectuem els quocients entre un terme i el seu anterior s’observa que:

1/1 = 1

2/1 = 2

3/2 = 1,5

5/3 = 1,66666

8/5 = 1,6

13/8 = 1,625

21/13 =1,615

.......................            

És a dir, que ens acostem al nombre d’or: 1,6180339...!

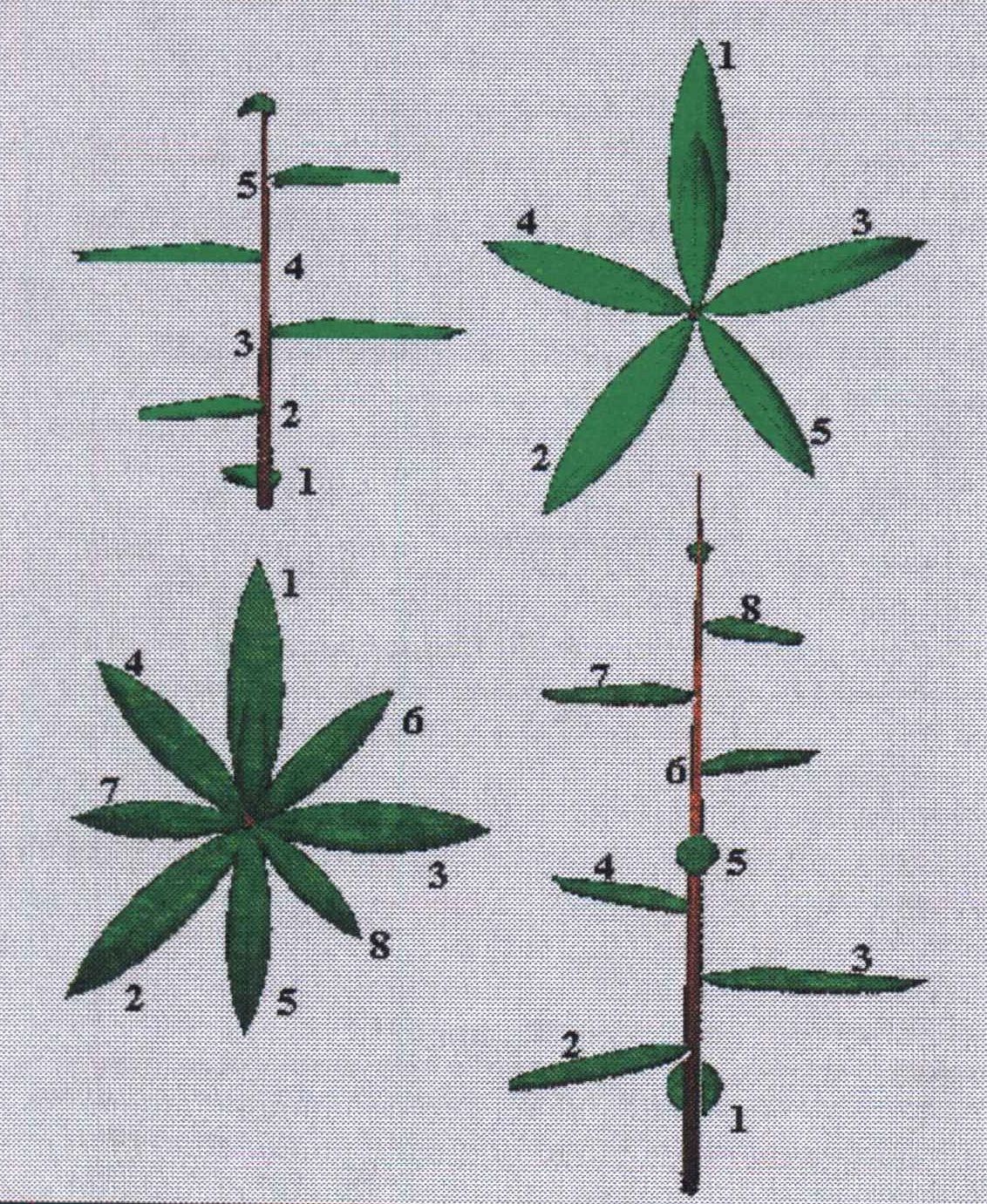
Aquesta meravellosa seqüència també la trobem a la natura, per exemple, en pinyes i fulles.

Així, en les pinyes si comptem les espirals que fan els pinyons en un sentit o en un altre, són sempre nombres diferents i a més són dos termes consecutius de la successió de Fibonacci.

I pel que fa a les plantes, si considerem dues branques amb fulles que estiguin a la mateixa tija (la mateixa vertical), entre ambdues hi ha un nombre de branques i fulles de la successió de Fibonacci.

També trobem exemples del nombre d’or i la successió de Fibonacci en llibres, televisió i, per descomptat, en l'art.

A la pàg. 61 de la novel·la de Dan Brown El codi Da Vinci apareix una versió desordenada dels primers vuit nombres de Fibonacci (13, 3, 2, 21, 1, 1, 8, 5), que funcionen com una pista deixada pel vigilant del museu del Louvre, Jacques Saunière.  En les pàgines 121-123 explica algunes de les aparicions d'aquest nombre (1,618) en la natura.

En l'episodi "Sabotatge" de la sèrie de televisió NUMB3RS (primera temporada, 2005), el geni de la matemàtica Charlie Eppes esmenta que el nombre d’or es troba en l'estructura dels cristalls, en l'espiral de les galàxies i en la petxina del Nautilus.

A la pel·lícula de Darren Aronofsky  Pi, fe en el caos el personatge central, Max Cohen explica la relació que hi ha entre els nombres de Fibonacci i la secció àuria, encara que denominen incorrectament el nombre d’or com a Theta en comptes de Phi.  

Finalment, en el moviment artístic italià arte povera dels anys 1960, moltes de les obres es basen en aquesta successió.