Les matemàtiques del GPS

Exposarem un senzill model matemàtic que ens aproxima i ens ofereix una lleugera idea de com treballa un GPS i que ens ajudarà a entendre la importància de la matemàtica en aquesta tecnologia.

Què és un GPS?

Els anomenats GPS (sistema de posicionament global) ens determinen la posició d’on som i d’on volem anar a partir d’una xarxa de 28 satèl·lits distribuïts pel cel, és a dir, que ens permeten saber amb molta precisió la situació geogràfica nostra i dels altres.

Els orígens del GPS (originàriament, NAVSTAR Global Positioning System o NAVSTAR GPS) es remunten a l’any 1978, quan es va llançar el primer satèl·lit de proves. Reservat per a usos militars dels EUA, el sistema no va ser plenament operatiu fins al 1994. A partir del 2 de maig del 2000 es va permetre la seva utilització civil.

Els satèl·lits que conformen el sistema GPS estan distribuïts en 6 òrbites a uns 20.000 km de distància que giren al voltant de la Terra cada 12 hores. Cada satèl·lit mesura 5 m de llarg i pesa 860 kg. Funcionen amb un sistema de plaques solars, i estan equipats amb un transmissor que pot rebre i emetre senyals codificats i un rellotge atòmic de cesi de gran precisió (es retarda 1 segon cada 30.000 anys).

GPS i matemàtiques

La idea matemàtica inicial és determinar la localització d’un cert punt, P, en certes condicions. Inicialment, sabem que aquest punt P està situat a una distància, per exemple, de 3 unitats d’un altre punt A conegut. Notem que qualsevol punt que estigui a una distància de 3 unitats de A estarà a la circumferència de centre A i radi 3 i, per tant, en principi, qualsevol d’aquests punts de la circumferència és candidat a ser P.

D’altra banda, també disposem d’informació que P és a una distància, per exemple, de 2 unitats d’un punt B conegut. Notem que els punts que verifiquen aquestes condicions estan respectivament a les circumferències de centre el punt A i radi 3 i a la circumferència de centre el punt B i radi 2, i, per tant, estaran simultàniament en les dues circumferències.

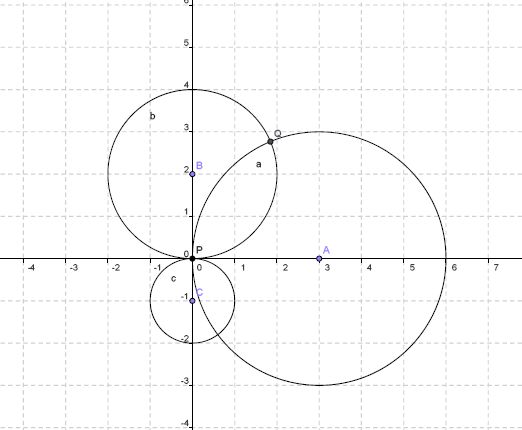
Amb aquestes condicions tenim dos candidats, P i Q, i no podem concretar quin és el buscat, així que caldrà conèixer un tercer punt C que, per exemple, disti 1 unitat d’algun d’aquests punts P i Q, per tal de determinar el punt en qüestió. Mostrem gràficament la situació:

Geomètricament, estem calculant la intersecció de tres circumferències, en l’exemple el punt A és el (3,0), el B el (0,2) i el C el (0,-1), on P és l’origen de coordenades. La construcció i recerca del punt P és un cas particular que s’anomena triangulació.

En el nostre exemple, els punts A, B i C són satèl·lits i el punt P és el punt que introduïm en l’aparell per esbrinar-ne la posició. Per determinar les distàncies s’utilitza la coneguda relació espai recorregut = velocitat x temps, de manera que l’espai recorregut correspon a la distància recorreguda pels senyals emesos entre l’aparell GPS i cada satèl·lit. El temps del senyal per recórrer aquest trajecte està determinat pels rellotges de l’aparell i els satèl·lits i la velocitat del senyal és la velocitat de la llum (300.000 km/s). Les distàncies són calculades, doncs, per l’aparell. Amb aquesta informació ja podem calcular P.

Cal aclarir que l’aparell GPS, de manera interna, calcula les coordenades de P respecte als punts A, B, C i el que mostra en pantalla és la correspondència entre P i el mapa de què disposa el GPS; evidentment, cal actualitzar regularment el mapa per tal de no perdre’ns!!!

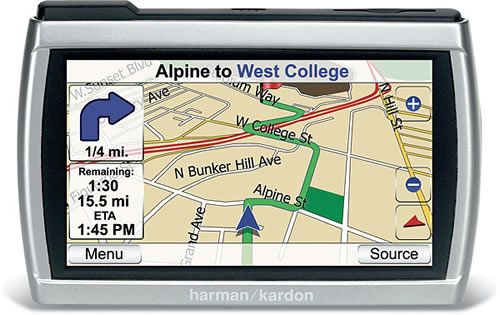
De fet, el que s’anomena triangulació consisteix a determinar les distàncies des de cada punt (notem que en general A, B, C són tres vèrtexs d’un triangle) al punt P per tal de calcular explícitament les coordenades d’aquest punt:

on A, B i C són coneguts i les distàncies r₁, r₂, r₃ també són conegudes. Geomètricament, estem calculant la intersecció de tres circumferències.

En síntesi i d’una manera més col·loquial podem afirmar que el GPS localitza automàticament com a mínim quatre satèl·lits de la xarxa, dels quals rep uns senyals indicant la posició i l'“hora” que indica cadascun d’aquests. Sobre la base d’aquests senyals, l’aparell sincronitza el rellotge del GPS i calcula el retard dels senyals, és a dir, la distància al satèl·lit. Per "triangulació" (determinar la distància de cada satèl·lit respecte al punt de mesurament), calcula la posició en què aquest es troba. Conegudes les distàncies, es determina fàcilment la mateixa posició relativa respecte als tres satèl·lits. Coneixent a més les coordenades o posició de cadascun d’aquests pel senyal que emeten, s’obté la posició o coordenades reals del punt de mesurament. També s’aconsegueix una exactitud extrema en el rellotge del GPS, similar a la dels rellotges atòmics que des de la Terra sincronitzen els satèl·lits.

Hi ha qüestions de caràcter més tècnic que no tractarem aquí, com són la sincronització horària dels satèl·lits i de l’aparell, o que els satèl·lits i “el vehicle en què circulem” estan habitualment en moviment, a més del fet que en realitat estem en tres dimensions (el model matemàtic i el raonament mostrats estan pensats en dues dimensions).