Els puzles, la nanotecnologia i l'emergència climàtica

Com és ben sabut, un puzle és un trencaclosques que té per objectiu construir una làmina o objecte 3D a partir de la juxtaposició de moltes petites peces que inicialment estan separades. Jo de petit tenia trencaclosques elementals, el típic conjunt de 12 o 24 cubs amb dibuixos per les sis cares, i que havies de muntar. El nom de trencaclosques –o el seu equivalent en castellà rompecabezas– és notable, en canvi puzle és més neutre i menys dramàtic.

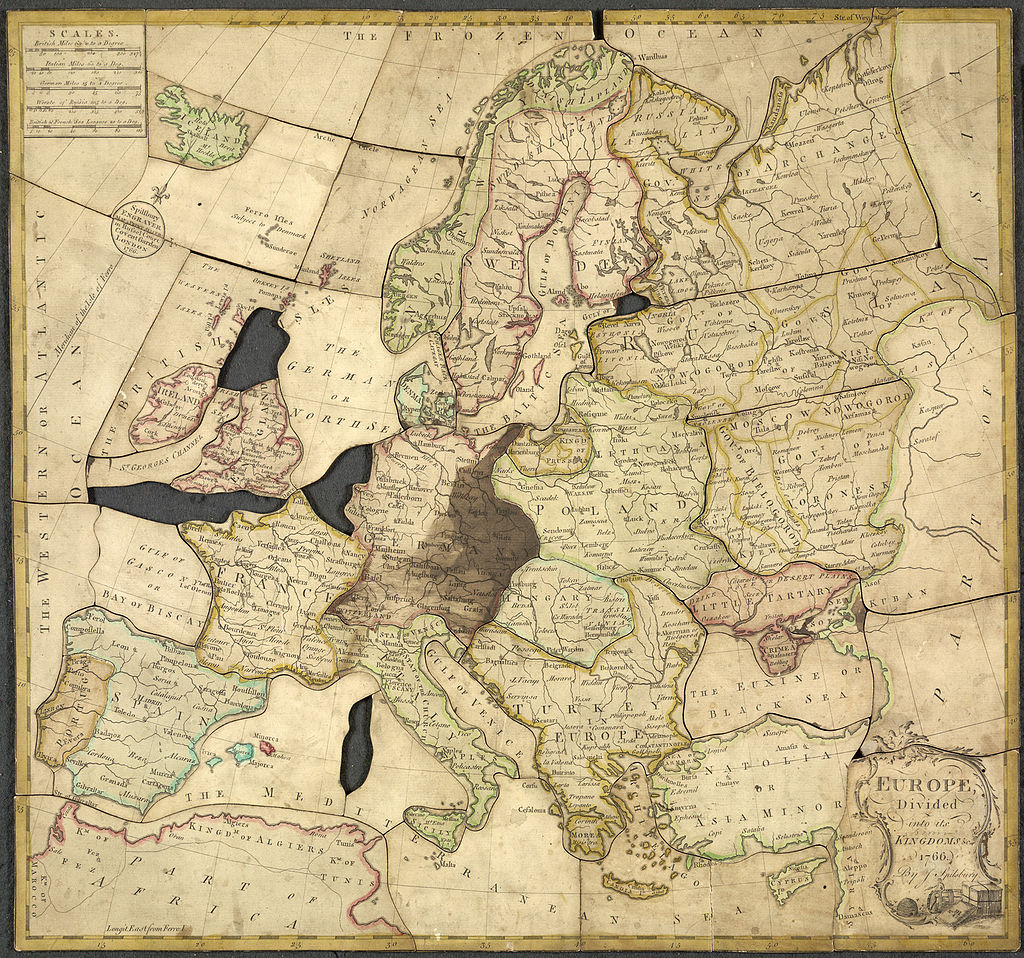
Centrem-nos en els puzles de peces petites que s’enganxen pels entrants i sortints. Sembla que el primer puzle és del 1760, fet a mà tallant fusta prima amb una serra de marqueteria, i representava el mapa d’Europa. Va ser fet per John Spilsbury a Londres, i tenia una finalitat educativa. Del nom de l’instrument usat per construir-lo, la serra de marqueteria, en deriva el nom en anglès, jigsaw. Ara se’n segueixen fent de fusta, i de plàstic, però la gran majoria són de cartró. En anglès, tant jigsaw com puzzle són alhora noms –una serra i un trencaclosques– i verbs: tallar amb una serra de marqueteria, i posar algun problema, respectivament [+].

En aquest moment el mercat mundial de puzles és enorme, i hi ha moltes empreses que en treuen diversos models cada mes, de totes les temàtiques i mides. N’hi ha en 2D i en 3D, rectangulars, circulars, ovalats, per no entrar en el món dels puzles virtuals. N’hi ha un, que no he vist, en què ets a l’interior del puzle i has d’anar-lo construint al voltant teu, fins que quedes dins del tot. Hi ha puzles infantils de dues peces en endavant. Es considera que des de 250 o 500 ja són puzles per a adults. Els més comuns són de 500, 750 i 1.000 peces. També n’hi ha de 1.500, 2.000, 3.000 i 4.000 peces, i cada fabricant té algun model de mides més grans, que li dona prestigi i així se’n parla. Durant un temps el puzle d’Educa de 42.000 peces i 11,76 m² de superfície, que és al mercat des del 2017, va ser el més gran del món. Se segueix venent per uns 350 €. Però el va superar el de l’empresa Martin Puzzle, de Txèquia, el 2018, que va ser el primer puzle de més de 50.000 peces. En concret té 52.110 peces, i ocupa 14,06 m². El venen per uns 300 € i pesa 23 kg. Però el puzle més gran que s’hagi fet mai –fins al 2018– es va muntar a Barcelona el 19 de setembre de 1993 per commemorar l’aniversari dels Jocs Olímpics. Amb una certa trampa, perquè consistia en més de 7.000 puzles de 1.000 peces cadascun i que es van juxtaposar després. Total, 2.400 m² i 843.552 peces. Hi van participar 14.000 voluntaris, i ho va dissenyar l’empresa DISET, ja desapareguda. El 2008 a Ravensburg van fer un puzle més petit, però amb 1,14 milions de peces, i el 2018 a Dubai van fer un puzle de només 12.320 peces de fusta, però cadascuna tenia la mida d’un puzle de 1.000 peces. Tenia 6.000 m² i va servir per honorar el xeic Zayed bin Sultan al-Nahyan, fundador dels Emirats Àrabs Units.

Quantes peces té realment un puzle?

Potser pot sorprendre –a mi m’ha sorprès– que en moltes ocasions el nombre de peces d’un puzle no és exactament el que diu la caixa. Ara fa poc hem acabat de muntar a casa un puzle de 1.000 peces, que pots veure aquí [+]. Efectivament en tenia 1.000, no perquè les comptéssim inicialment, sinó perquè consta de 40 files i 25 columnes. Però en altres casos els puzles "de 1.000 peces" tenen 1.026 peces (38 files i 27 columnes); els puzles "de 2.000" en solen tenir 2.000, però a vegades 1.998. I els de 3.000 en tenen 3.168. I els de 500 en tenen 500 (20 x 25) o 513 (27 x 19).

Per què passa això? És per un doble motiu, estètic i pràctic. En certes ocasions els fabricants volen que la mida del puzle muntat s’acosti al màxim a les proporcions fixades per les normes DIN, que són rectangles on el costat curt és la unitat i el llarg fa 1,41 vegades el costat petit. En un puzle de 2.000 peces exactes, i suposant que l’amplària de cada fila i cada columna fossin la mateixa, que és el més normal, s’han de distribuir en 50 files i 40 columnes o viceversa, però això dona unes proporcions del puzle de 50/40 = 1,25: seria un rectangle massa "quadrat". En canvi si hi ha 1.998 peces, es distribueixen en 54 files i 37 columnes, amb una proporció de 54/37 = 1,46, més similar a la proporció DIN. El mateix argument val per a la resta de mides de puzle. Si fos per motius estètics, els fabricants potser preferirien la raó àuria, que és 1,618.

Quantes peces hi ha a les vores d’un puzle. Una aproximació a la nanotecnologia

Quantes peces hi ha a les vores d’un puzle rectangular? El primer pas per començar un puzle és fixar-ne les vores, perquè són peces fàcils d’identificar. És fàcil de calcular el nombre de peces de les vores: és –gairebé evident– la suma del nombre de files i de columnes multiplicada per 2, i restant-ne 4 per evitar duplicar els vèrtexs. La llàstima és que, tenint en compte els paràgrafs anteriors, no sabem realment quantes peces té el nostre puzle, ni quantes files ni columnes, fins que és muntat, i par tant no podem calcular a priori quantes peces hi ha als costats, informació que per altra banda no ens serviria per a gairebé res.

És més interessant veure la relació entre el nombre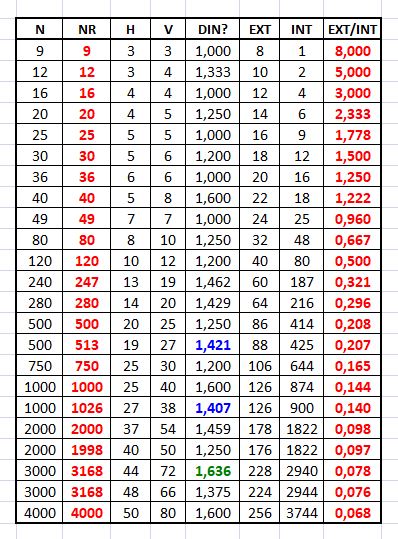 de peces de les vores i les de l’interior. Vegem la taula adjunta on hi ha les característiques de tots els puzles que hi ha o hi ha hagut a casa, des del més petit que té vora i interior, de 9 peces, fins al més gran que hem fet, de 4.000 peces. A la taula s’hi indica el nombre de peces nominal N, el nombre real NR –en vermell–, el nombre de files (H, d’horitzontals) i columnes (V, de verticals) –o viceversa, segons el puzle–, el quocient V/H per veure si les dimensions s’aproximen a les DIN o a la raó àuria, quantes peces hi ha a les vores (EXT), quantes a l’interior (INT), i la raó entre peces exteriors i peces interiors EXT/INT. Veiem que les mides de puzle més properes al format DIN són els de 500 i 1.000 peces nominals, peces reals 513 i 1.026; i el més proper a la raó àuria és el de 3.000 peces, realment 3.168.

Com era fàcil d’intuir, als puzles petits hi ha més proporció de vora que als grans. Un puzle quadrat de 9 peces, el més petit que pot tenir vora i interior, té 8 peces de vora i només 1 d’interior. La raó EXT/INT és tan alta com 8, la màxima possible. El puzle de 40 peces és el darrer dels que té encara més peces a la vora (22) que a l’interior (18). A partir d’aquí n’hi ha més dins que a la vora, des del de 49 (24 i 25) fins al darrer dels que tinc dades, el de 4.000, que té 256 peces a les vores i 3.744 a l’interior.

Què té a veure tot això amb la nanotecnologia, la tecnologia de partícules i les emulsions? Aquests tres camps tecnològics es basen en una propietat comuna: la matèria finament dividida té propietats que són diferents de la matèria agrupada en partícules grosses. Una goteta de perfum en aerosol molt petita té una proporció de molècules a la seva superfície superior a una goteta més grossa. A causa de fenòmens físics que no detallarem, i relacionats amb el radi de curvatura, la pressió de vapor del líquid de les gotetes petites és més alta que la de les gotetes grosses, i per això el perfum es nota més en aerosols molt fins: s’evapora més ràpidament i es difon millor a l’ambient. De forma similar, en un material sòlid soluble, com una sal, els cristallets molt petits tenen una proporció superior de superfície a volum, i això fa que es dissolguin més de pressa I, tercer exemple, un catalitzador sòlid es basa a adsorbir molècules del reactant a la seva superfície interior i als porus, i allà reaccionen. Com més petita sigui la partícula, més àrea superficial tindrà i la reacció podrà ser més ràpida.

Imaginem el puzle de 2.000 peces reals, però repartit en 100 puzles de 20 peces cadascun. Hauríem passat d’un únic puzle de 178 peces de vora i 1.822 d’interior, a un conjunt de 100 minipuzles amb 2.800 peces a les vores i 1.200 a l’interior: hem multiplicat per gairebé 24 la superfície exterior. I això que tenim en compte només les dues dimensions dels puzles. Si parléssim de partícules 3D, la relació entre l’àrea exterior i el volum augmenta més de pressa, naturalment. Un cub d’1 m³ té una àrea superficial de 6 m², però si fem un milió de cubs d’1 cm de vora tindran 600 m² de superfície: l’hem multiplicat per 100. I quan passem a dimensions nanomètriques, l’àrea superficial es multiplica enormement: aquest mateix cub dividit en nanocubets d’1nm d’aresta passaria a tenir mil milions de m² de superfície. Emulsions, nanopartícules i catalitzadors tenen les aplicacions que tenen per la seva elevada relació de superfície a volum.

La resolució de puzles, un atemptat ecològic?

Un puzle és un objecte ja construït, una làmina de cartró, que el fabricant trenca en trossets de mida arbitrària, que barreja, i que després l’usuari ha de tornar a ajuntar com era al començament. En el procés es consumeix energia i s’incrementa l’entropia de l’univers d’una manera aberrant: teníem un conjunt ordenat, el desordenem i el tornem a ordenar. L’ordenació requereix un notable esforç intel·lectual, i per tant un notable consum de glucosa al cervell. Cal mirar les propietats de cada peça, i això peça per peça, trobar-hi regularitats i després trobar les juxtaposicions òptimes. Calcular, a partir del nombre de peces, l’increment d’entropia de l’univers que cal per resoldre un puzle no es pot fer de manera fàcil, i és millor calcular-ho a partir del temps mitjà que es tarda a resoldre’l.

Quant es tarda a resoldre un puzle? Naturalment, depèn de la persona. Mirem els campions. Hi ha molts campionats de resolució de puzles, que es basen a subministrar als concursants el mateix puzle i veure quant tarden a resoldre’l. Aquí [+] es poden trobar les dades del Campionat d’Espanya del 2019, darrer dels celebrats, a Aranjuez el 15 de juny. Hi van participar 262 inscrits. La guanyadora va ser Lina Ivanova, de Novosibirsk (Rússia), que va resoldre el puzle de 500 peces en... 38 minuts i 42 segons (!). Com a consol, la darrera classificada va aconseguir posar 69 peces en 2 hores 30 minuts, temps màxim de la prova. Hi va haver 200 participants, però, que van aconseguir completar el puzle en aquest temps. El primer –i per ara darrer– campionat mundial es va celebrar a Valladolid el 2019, i els temps que van gastar els millors van ser similars. [+]

La resolució d’un puzle requereix energia. El cervell consumeix aproximadament 5,6 mg de glucosa per cada 100 g de teixit cerebral i per minut. En un cervell mitjà, d'1,5 kg, la resolució d’un puzle –o de qualsevol altra activitat pensant– requereix 84 mg de glucosa per minut. Si tardem una hora a resoldre un puzle de 500 peces, això són 5 g de glucosa. Si aquesta glucosa prové del sucre que mengem, aproximadament necessitem un sobret de sucre de cafè per resoldre el puzle. I l’oxigen corresponent per oxidar la glucosa i subministrar l’energia metabòlica. No és gaire. Equival a 15 vats, una bombeta LED normal. I resoldre el puzle en una hora serien 54 kJ. Però és energia llençada, perquè el puzle ja estava muntat i voluntàriament l’han desmuntat i nosaltres el tornem a muntar. És una pèrdua de temps i d’energia, en resum.

Però això ja ho sabíem. Tot el que es fa per plaer és el mateix. També és un dispendi d’energia una muntanya russa, que ens eleva al cel i després la gravetat ens torna a allà mateix d’on hem sortit. És malbaratar energia anar a un gimnàs a fer esforços que, tot plegat, acaben escalfant l’aire per la respiració i escalfant les màquines de tortura. És malbaratar energia jugar a qualsevol esport. I mil exemples més. Si només haguéssim de fer allò que convé al medi, jo pararia ara mateix d’escriure i tu pararies de llegir. Ni jo ho faig perquè em calgui fer-ho, ni a tu et cal llegir. Però, on quedaria la vida humana sense els plaers físics o intel·lectuals. Viure amb una certa dignitat és malbaratar, però tampoc cal passar-se...

Vaig a caminar. També és malbaratar energia, però la salut m’ho demana: el difícil equilibri...