La taula periòdica, tan periòdica no és

L'ordenació periòdica amb els pesos atòmics

Mendeléiev va escriure un llibre que tenia per títol Principis de Química. És a dir, buscava principis, no només descriure. Hi buscava lleis bàsiques, i va descobrir el que se'n va dir la llei periòdica. Aquesta llei pretenia trobar una relació entre els pesos atòmics dels elements i les seves propietats. En aquell temps es coneixien 63 elements, amb els seus pesos atòmics força ben establerts. No es tenia cap indici de l'estructura de l'àtom. El pes atòmic —ara cal dir massa atòmica— era un valor no intuïtiu, que no tenia cap relació amb la densitat, contra el que podria semblar pel seu nom. Es coneixien ja grups d'elements afins, com els alcalins, els alcalinoterris, els calcògens (el grup de l'oxigen), els pnictògens (el grup del nitrogen), i els halògens. A cada grup els elements —les substàncies elementals, més exactament— tenien propietats físiques i químiques força semblants: el mateix caràcter, metàl·lic o no; les fórmules dels seus compostos amb l'oxigen o amb l'hidrogen, o el seu caràcter àcid o bàsic. També eren conegudes les tríades de Döbereiner i de Lenssen, que relacionaven de forma quantitativa els pesos atòmics d'elements més o menys anàlegs. La figura 1 mostra la vintena de tríades conegudes fins a 1857. Intenti, el lector, imaginar aquestes relacions, però sense el suport visual que li dona conèixer on estan avui situades a la taula periòdica, eina que no existia, i veurà que tenia mèrit trobar-ho.

Figura 1. Tríades de Döbereiner i Lenssen sobre una taula periòdica actual.

Les similituds entre elements d'un grup eren, doncs, ben conegudes, però això no era la periodicitat. La novetat de l'ordenació de Mendeléiev fou que, en posar els elements per ordre de pesos atòmics, va observar que també hi havia una certa periodicitat entre elements de grups diferents. És a dir, que, partint del liti, al cap de set elements hi havia un element similar, el sodi. I al cap de set elements més, un altre de similar, el potassi. I no només això, sinó que els elements intermedis entre liti i sodi, o entre sodi i potassi, mostraven una variabilitat regular de propietats. Domènech (2019) ens resumeix diversos exemples d'aquesta periodicitat. Per exemple, la sèrie dels òxids màxims dels elements consecutius és regular: Na₂O, Mg₂O₂ (MgO), Al₂O₃, Si₂O₄ (SiO₂), P₂O₅, S₂O₆ (SO₃) i Cl₂O₇. Es troben seqüències similars amb els productes de les reaccions dels òxids amb aigua, o amb les combinacions dels elements amb hidrogen.

En resum, l'ordenació per pesos atòmics en la taula de doble entrada de Mendeléiev de 1871 i totes les posteriors —grups verticals i períodes horitzontals—, mostra analogies entre els membres d'un mateix grup, i també regularitat de propietats físiques i químiques entre membres d'un mateix període. Aquesta és la llei periòdica, la de la regularitat de les propietats quan l'ordenació és per pesos atòmics. Mendeléiev estava convençut que aquesta llei periòdica era una llei bàsica de la naturalesa, i per això s'atrevia a deixar vacants alguns espais, o a modificar alguns ordres de pesos atòmics atribuint errors als experimentadors que els havien determinat. La llei periòdica es pot expressar gràficament en la forma d'un sistema periòdic d'elements, que és com se solia i se sol dir per part de molts autors a la representació gràfica. Però no tots: alguns experts identifiquen llei periòdica i sistema periòdic, que serien els conceptes abstractes, i que es plasmen en forma de taules periòdiques de disseny variat (Wang i Schwarz, 2009). Altres, en canvi, consideren que la llei és el concepte abstracte, plasmat en taules o sistemes periòdics: no distingeixen entre el sistema periòdic dels elements i la taula periòdica dels elements, conceptes considerats sinònims.

L'ordenació periòdica amb els nombres atòmics

El descobriment de l'electró, del protó i posteriorment del neutró van permetre postular les configuracions electròniques dels àtoms de cadascun dels elements. No casualment l'ordre de pesos atòmics coincideix quasi exactament amb l'ordre dels elements per nombres atòmics, perquè l'increment del nombre de protons dels nuclis és acompanyat per l'increment del nombre de neutrons de forma quasi proporcional, en la major part d'isòtops dels elements.

Quan l'àtom deixa de ser una caixa negra, es pot intentar trobar una relació entre nombre atòmic i propietats dels elements i de les substàncies elementals. Efectivament, el nombre atòmic ens permet deduir l'estructura electrònica de l'àtom i d'aquí veure els electrons de valència, deduir l'estructura molecular o iònica de la substància elemental i dels compostos en què participa un àtom, i per tant, es pot fer una interpretació de les seves propietats. La posició en la nova taula periòdica construïda a partir del nombre —la primera, la de Langmuir el 1919 i després tota la resta— ens informa, doncs, de les propietats de l'element; no és simplement una ordenació feta a partir d'alguna propietat ja coneguda de l'element, com era la taula periòdica basada en el pes atòmic.

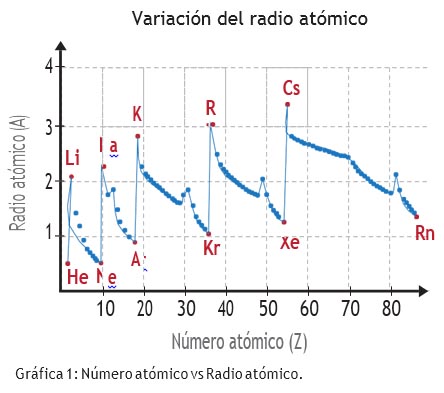
Figura 2. Variació periòdica del radi atòmic amb el nombre atòmic.

Es poden explicar, així, la major part de les propietats, i els llibres de text avançats així ho fan de forma qualitativa. Vegeu, per exemple, Atkins (1989) a través d'algun exemple. Per què el radi atòmic —que és un valor experimental— augmenta en baixar per un grup? Perquè a cada nou període hi ha electrons que ocupen espais més allunyats del nucli. I per què disminueix el radi atòmic al llarg d'un període? Perquè el nucli és cada cop més positiu, atreu els electrons amb més força, i fa l'àtom més compacte (figura 2). Raonaments similars es poden fer per al radi iònic. Els cations són de radi més petit que l'àtom neutre perquè han perdut electrons externs. El radi dels cations augmenta en baixar per un grup per la mateixa raó que augmenta el radi atòmic. Els anions són de radi més gran que l'àtom neutre perquè hi ha més electrons al nivell de valència, que es repel·leixen entre ells. Si comparem els ions isoelectrònics Na⁺, F^- i Mg²⁺, observem que aquest darrer és el de radi iònic més petit: el seu nucli té més càrrega i atreu més els electrons. En canvi F^- té més electrons que protons, es repel·leixen més i té el radi iònic més gran. I el mateix raonament val per als potencials d'ionització, l'energia requerida per arrencar electrons de l'àtom neutre: en general es redueixen en baixar per un grup, perquè els electrons de valència estan més llunyans. En canvi, augmenten en general en avançar per un període perquè hi ha més càrrega nuclear. Així doncs, cada propietat d'un àtom pot relacionar-se amb la seva configuració electrònica, i de fet aquest és un dels objectius dels estudis teòrics i experimentals de la química avui, objectiu encara molt lluny d'haver-se aconseguit.

Les consideracions anteriors són totes qualitatives i no gaire acurades. Si fem un pas més, veiem que la taula periòdica està ara estructurada en blocs, corresponents cadascun a un nivell d'electrons. Així, al bloc s, format pels grups 1 i 2, els electrons determinants del comportament de l'àtom són els s més externs, mentre que tota la resta d'electrons són de nivells interns i no tenen tanta influència en les propietats de l'àtom. Al bloc p (grups del 13 al 18), els electrons determinants són els s i els p més externs, i la resta d'electrons són més interns i no influeixen gaire en les propietats de l'àtom. Al bloc d (grups del 3 al 12) la presència d'electrons d a aquest nivell condiciona el comportament dels electrons s més externs, perquè a aquest bloc no hi ha electrons p externs. Finalment, els elements del bloc f (lantànids i actínids) tenen electrons externs s una mica condicionats per la presència d'electrons f més interns, però que tenen menys influència que la que tenen els electrons d en els elements del bloc d. Tot plegat matisa i en part explica els comportaments indicats al paràgraf anterior. La regla de Madelung —o regla de Moeller, o regla del xerrac, o principi de construcció, o principi d'Aufbau— Intenta donar una pauta per saber a quin nivell són on els electrons de cada element.

Però tampoc aquesta pauta, que d'entrada sembla molt regular, molt comprensible i que és apresa amb entusiasme pels alumnes, és certa. És només una aproximació a la realitat. El fet és que entre els electrons d i els f hi ha poca diferència d'energia i això fa que les excepcions siguin moltes. Dels 64 elements dels blocs d i f entre Z=21 (Sc) i 108 (Hs) hi ha 21 casos en què la regla de Madelung no prediu la configuració electrònica real. Les configuracions amb s²d⁴ o s²d⁹ són menys estables que les s¹d⁵ o s¹d¹⁰, per exemple, i són aquestes darreres les que es troben a la realitat. Els elements en els quals això passa, i els seus compostos, tenen propietats que no quadren amb la periodicitat regular esperada. Aquest és el cas de Cu, Cr, Pd, Ag, Rh, Pt, Au o U, per citar-ne alguns.

La manca de periodicitat de la taula periòdica

Qualsevol taula periòdica aspira a presentar de forma òptima el comportament i les propietats dels elements i/o de les substàncies elementals. És una plasmació gràfica de la relació entre propietats i configuració electrònica citada a l'apartat anterior. Però les propietats que podem observar en un element o en una substància elemental són dotzenes o centenars, i no sempre s'aprecia la periodicitat en una simple representació en dues dimensions, com la de les taules periòdiques clàssiques. Com destaquen Wang i Schwarz (2009) s'han fet anàlisis dels valors numèrics de més de 150 propietats de fins a 103 elements, i del conjunt no es mostren gaires regularitats i, per descomptat, no es dedueix la manera òptima d'organitzar els elements en forma de taules periòdiques bidimensionals, si es vol tenir en compte la representació de diverses propietats alhora.

Hi ha estudiosos que fan propostes summament complexes de formes de taules periòdiques, moltes d'elles multidimensionals, per poder arribar a incloure més propietats i més relacions. S'han presentat més d'un centenar de taules tridimensionals, començant pel vis téllurique de Chancourtois —de 1862, d'abans de Mendeléiev— fins als cilindres d'Ishiguro (2019), i fins i tot alguna en pseudoquatre dimensions. Vegeu-les al web de Chemogenesis (2019) on es presenten més de mil taules de tot tipus.

Però quasi tothom prefereix, per simplicitat, usar la taula periòdica bidimensional clàssica, ordenada per nombres atòmics, sigui en el format curt o el llarg. Naturalment, les regularitats que hi ha a aquesta taula són les que ja apareixien en les taules periòdiques basades en pesos atòmics: els dos grups principals -1 i 2- de metalls de l'esquerra i els sis grups de metal·loides i no metalls —incloent-hi els gasos nobles— de la dreta, dels 13 als 18. Aquests grups mostren les afinitats de propietats ja conegudes per Mendeléiev i abans. Però hi ha altres regularitats, com els químics han anat descobrint, que no estan contingudes als grups ni als períodes de la taula periòdica habitual. A la figura 3 es poden constatar alguns exemples de parelles o altres conjunts d'elements que mostren propietats similars. Aquests fets em van sorprendre en estudiar i traduir el llibre d'Atkins citat, que les destaca.

Així, s'hi han trobat diverses connexions diagonals, que són les similituds que mostren certs parells d'elements que són de dos grups i dos períodes consecutius. Per exemple, les similituds entre Li i Mg, O i Cl, o entre Be i Al, aquests aparentment distants pel buit que el bloc d genera a la taula. Qualitativament s'explica aquesta similitud per les pautes de tendència que mostren els radis atòmics comentades abans, i els potencials d'ionització que també s'assemblen en diagonal. La franja que separa metalls de metal·loides és també una clara diagonal. Hi ha també connexions distants, com entre Al i Fe, o entre Ba i Pb. Hi ha conjunts connectats, com el rectangle de sis metalls entre Ru i Pt. Hi ha també relacions de salts de cavall i fins i tot salts de cavall encadenats. Són els que relacionen Zn i Sn, Ag i Tl, Cd i Pb i Ga i Sb, parells d'elements que mostren força similituds, especialment pel que fa als seus compostos anàlegs. No hi ha encara, sembla, explicacions quantitatives convincents per a aquests comportaments.

La contracció dels lantànids, descrita de fa temps, és el concepte que explica per què els radis atòmics dels metalls del període 5 són més grans que els del període 4, però en canvi els del període 6 són com els del període 5. S'interpreta aquest comportament perquè al llarg dels lantànids —de La a Lu— es va reduint el radi atòmic, per la càrrega nuclear creixent i el pobre efecte apantallant dels electrons f. Això explica també l'alta densitat dels metalls de transició del període 6 que venen a continuació. També explica la baixa reactivitat d'Au i Pt, a la dreta dels metalls de transició del període 6: els seus electrons de valència són prop del nucli i atrets fortament.

Hi ha encara altres aspectes de no periodicitat clàssica, com algunes de les citades en un post anterior [+]. Per exemple, la discussió sobre on haurien d'anar l'hidrogen i l'heli, quins són els elements del grup 3, o per què els primers elements de cadascun dels grups principals són força diferents dels elements de la resta del seu grup.

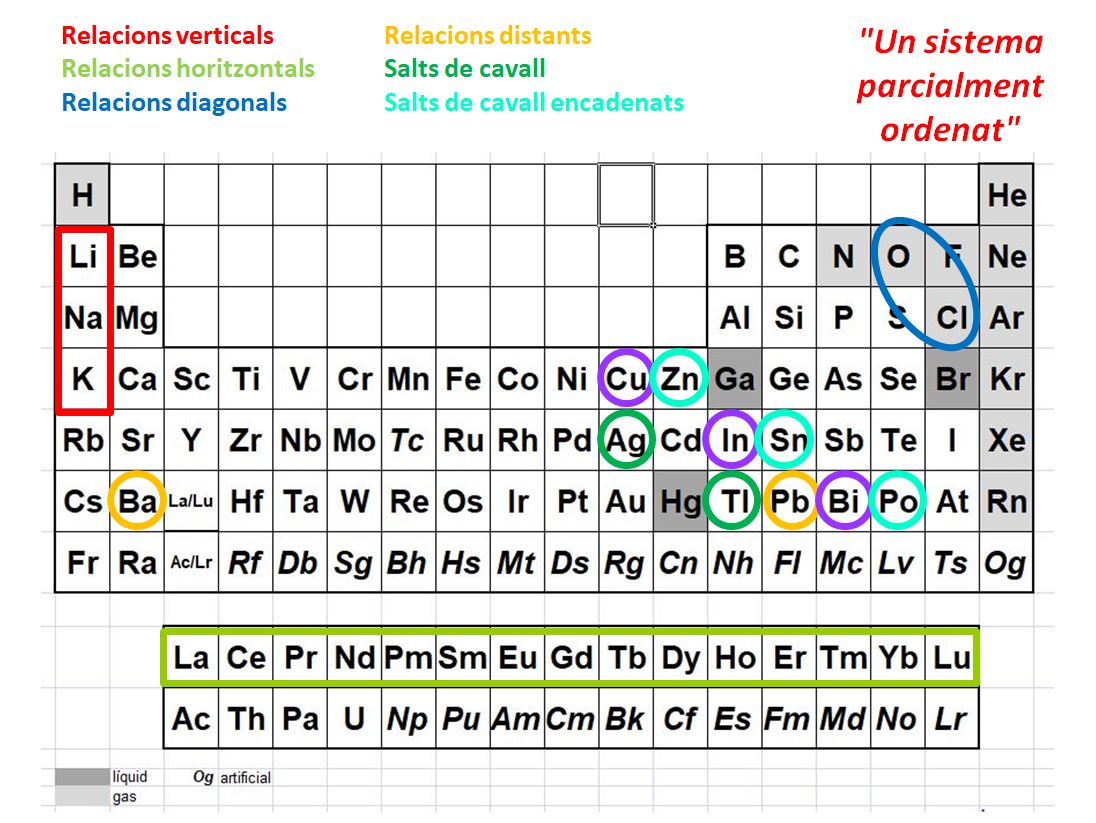
Figura 3. Relacions convencionals i no convencionals entre elements.

Resum final

Les taules periòdiques inicials es basaven en els pesos atòmics, i contenien només la meitat d'elements que les actuals. Mostraven al llarg dels grups principals les similituds dels elements, i al llarg dels períodes la periodicitat de certes propietats. L'ordenació per nombre atòmic va donar més profunditat al model, en poder relacionar les propietats atòmiques amb les configuracions electròniques. Però la capacitat d'ordenació i de relació es va anar desdibuixant a mesura que va augmentar el nombre d'elements coneguts, i sobretot quan es van voler relacionar moltes més propietats químiques i físiques. Per aconseguir-ho es van dissenyar una enorme varietat de taules. La forma de taula curta, majoritàriament usada, mostra els grups principals —blocs s i p— i els primers períodes aproximadament com ho feien les taules de fa cent cinquanta anys. Però la periodicitat es perd força en els elements del bloc d, i les relacions de similitud ja no són tan fàcils de trobar. Ara per ara, "el conjunt d'elements visualitzats per les taules periòdiques formen un sistema parcialment ordenat", com va dir Klein als anys noranta. Els químics teòrics tenen feina a fer.

REFERÈNCIES

Atkins, Peter; Jones, Loretta (1989). Chemistry: molecules, matter and change. W.H.Freeman, Nova York. Traduït (1998, 3a edició) Ediciones Omega, Barcelona.

Domènech, Josep Lluís (2019). La taula periòdica: més enllà d'una ordenació d'elements, Daualdeu, solstici d'estiu de 2019, p. 44-51.

Ishiguro, Takehiko (2919) https://www.youtube.com/watch?v=AL6tBrhju4Q

Klein , D.J (1995) J. Math Chem. 18, 321-348. Citat per Wang i Schwarz (2009).

Leach, Mark R.(2019) Web Chemogenesis https://www.meta-synthesis.com/webbook/35_pt/pt_database.php 

Leach, Mark R.(2019) Web Chemogenesis https://www.meta-synthesis.com/webbook/35_pt/pt_database.php?Button=3D+Formulations

Scerri, Eric R. (2006) What if the periodic table starts and ends with triads? PhilSci Archive http://philsci-archive.pitt.edu/3095/

Scerri, Eric R. (2007) The Periodic Table. Its Story and Its Signifiance. Oxford University Press.

Scerri, Eric R. (2011) The Periodic Table. A Very Short Introduction. Oxford University Press. Traduït: La tabla periódica: Una breve introducción, Alianza Editorial, El Libro de Bolsillo (2013).

Wang, Shu-Guang, Schwarz , W.H.Eugen (2009) Icon of Chemistry: The Periodic System of Chemical Elements in the New Century. Angew. Chem. Int. Ed. 2009. 48, 2-14.