
Les matemàtiques del contagi: epidèmies i altres models exponencials
-
- Home
-
- 9 of 21
Escalfant motors: un cas hipotètic
A tall d'exemple, s'introdueix una hipotètica situació de contagi per tal d'establir una aproximació a algun tipus de model matemàtic que simuli el comportament d’una epidèmia. Per fer-ho, suposem que un individu encomana només tres persones i l'endemà cadascuna d'aquestes tres persones contagia només tres persones més i així successivament. Tindrem la següent situació:
|
Contagiats el primer dia |
Nous contagiats el segon dia |
Nous contagiats el tercer dia |
Nous contagiats el quart dia |
Nous contagiats el dia n |
|
|
1 |
3 |
9 |
27 |
3 n-1 |
|
|
Total contagiats al primer dia |
Total contagiats fins al segon dia |
Total contagiats fins al tercer dia |
Total contagiats fins al quart dia |
Total contagiats des del dia 1 fins al dia n |
|
|
1 |
4 |
13 |
40 |
\({{3^n-1} \over 2}\) |
En general si el primer terme el denominem (en l’exemple
i la raó de creixement la denotem r (en termes matemàtics s'anomena raó i en termes mèdics es denota
), s'obté el model
, on el terme
indica el nombre de persones que s'han infectat el dia n i l'expressió
indica el total d'infectats des de l'inici fins al dia n. Es pot avançar que de forma discreta el model segueix el patró habitual d'una progressió geomètrica.
L'exemple anterior permet realitzar preguntes del tipus: El desè dia quants infectats hi haurà? I el total d'infectats des del primer dia fins al desè? Quants dies han de passar, si no es prenen mesures, per tenir un total de 100.000 infectats?
Un senzill càlcul ens apunta que el desè dia hi haurà infectats, essent el total d’infectats en aquests deu dies
. Si desitgem saber el temps que es trigarà perquè hi hagi 100.000 infectats, el model ens remet a la resolució de l’equació exponencial 100.000 =
, que té per solució (mitjançant l’ús de logaritmes, o una calculadora)11,1104; és a dir, passats 11 dies s’assolirà la xifra de 100.000 infectats.
Els resultats suggereixen algunes reflexions: Cal prendre mesures? De quina tipologia? El sistema sanitari està saturat? Aquestes reflexions són una petita lliçó per al lector de les conseqüències que pot ocasionar una epidèmia.
En l’expressió la variable n és un nombre natural, per tant és un model discret; aquest fet suggereix considerar el model de manera contínua introduint qualsevol valor temporal x i en tal cas podem establir el model més ampli com la funció:
, de manera més general tindrem una expressió de la forma:
.
La importància del valor és vital. Per visualitzar la gràfica del model prendrem, per fixar idees i per senzillesa, el valor K = 1 i en tal cas s’observarà el paper rellevant de diferents valors del paràmetre
en el control epidèmic.
Amb > 1 l’aspecte de la gràfica de la funció
és de la forma:
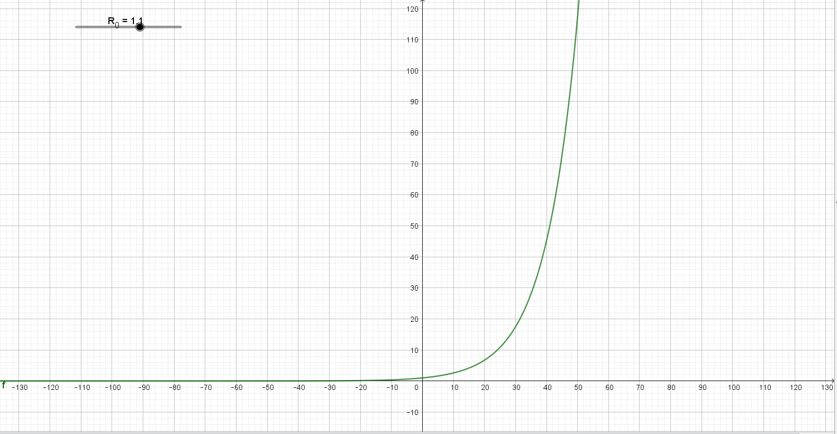
Amb de contagi epidèmic va disminuint:
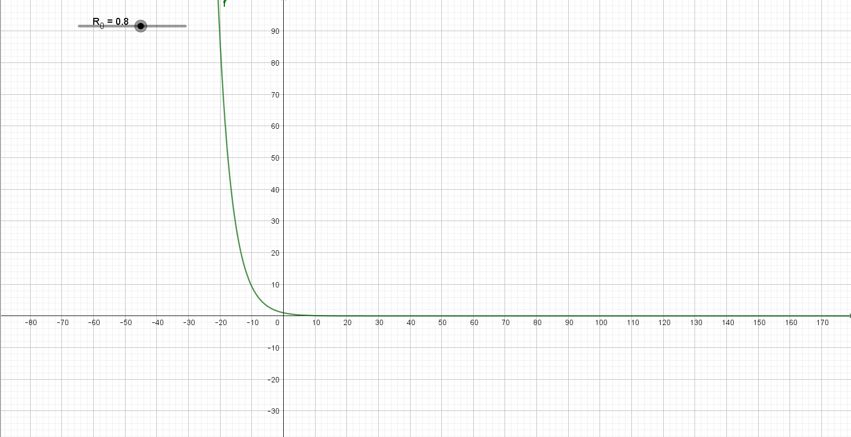
S’observa que el comportament de les corbes és força diferent en funció del paràmetre . El més important és poder disminuir el valor de
, perquè si és menor que 1 significa que cada persona no arriba a infectar una persona i la propagació s’atura per la dinàmica mateixa.
En síntesi, el model matemàtic formal vindria determinat en funció de dues variables independents: i el temps t. És evident que el valor
varia constantment (de fet és la velocitat de propagació) i el model el podem escriure com la funció de dues variables:
amb
Situacions reals. El cas particular de la covid-19
En diverses epidèmies s’ha comprovat experimentalment alguna aproximació al factor d’alguna tipologia de contagi epidèmic, tal com s’il·lustra en les següents imatges.
Segons les dades publicades per l'OMS, l'ECDC, el CDC i el British Medical Journal el 6 de febrer de 2020, tenim que en un primer cicle els elements A contagien els elements B, recordem que el nombre de contagis possibles a partir de cada element vindrà determinat pel factor .

Posteriorment tindrem que el creixement és de la forma
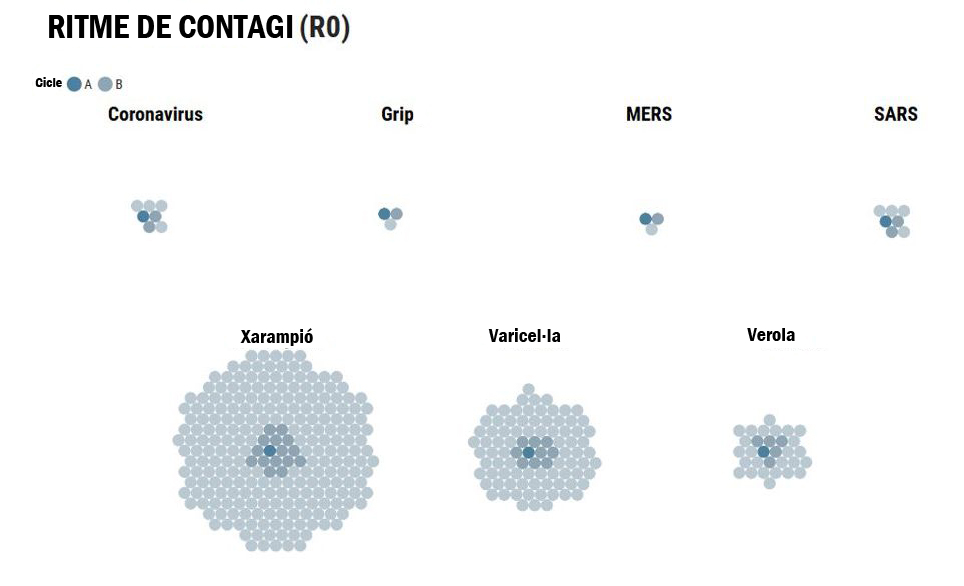
En l’esquema anterior s’aprecia el creixement provocat per cada virus.
Per al xarampió, per exemple, el s'estima al voltant de 15. És a dir, durant un brot de xarampió, una persona infectada n'encomana una mitjana de 15 més, si cap està vacunada. Per a la varicel·la, el
és aproximadament 10. En el cas del coronavirus l'estimació inicial de
és de 2,5. Si consultem les hemeroteques, la grip espanyola de l'any 1918 tingué un
de l'ordre de 2,1.
En la primera fase s'infecten cada vegada més persones i cada vegada més ràpid. La velocitat de contagi depèn, doncs, de la mida de i d'una altra variable fonamental, el temps que transcorre entre el moment en què una persona s'infecta i el moment en què aquesta mateixa persona n'infecta una altra. En el cas de la covid-19 s'estima que aquest temps és d'entre 4 i 14 dies.
- La principal preocupació en aquests moments és reduir el valor de
, aquesta disminució provoca que la velocitat d'expansió va més lenta. I quan
es comporta per sota del valor crític d'1, la difusió comença a aturar-se. A partir d'aquest moment, és l'epidèmia mateixa la que s’asfixia.
Un dels principals problemes a escala sanitària és la saturació dels centres hospitalaris. El nombre de contagis que necessitin ingrés hospitalari pot ser superior a la capacitat dels centres sanitaris, per això és de màxima importància prendre mesures restrictives necessàries i adequades tal com mostra el model plasmat en el gràfic:
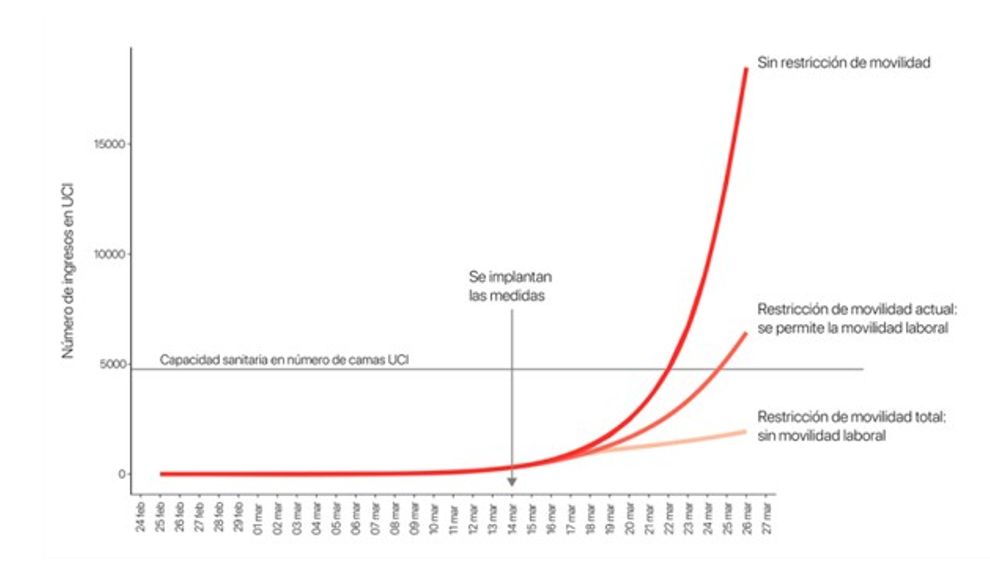
El model de Gompertz
Un model clàssic, de tipus exponencial, utilitzat en l'estudi de diverses epidèmies és l'anomenat model o corba de Gompertz, de Benjamin Gompertz (1779-1865), que serveix per preveure quin serà el comportament de l'epidèmia en els pròxims dies i setmanes; de manera que davant d'una situació nova com la d'aquest coronavirus, els models matemàtics són vàlids per a previsions a curt termini. Ve determinat per l'expressió:
o bé per
(model de Gompertz modificat), on el paràmetre a és el nombre inicial de cèl·lules/organismes quan el temps és zero (és a dir, en l'instant inicial del contagi); els paràmetres b i c depenen d'altres factors de tipus experimental. Cal notar que si b tendeix a infinit, la corba tendeix a zero, amb la qual cosa s'extingeix la pandèmia.
En la gràfica es mostra una petita aproximació realitzada amb el programa Geogebra de la corba de Gompertz:
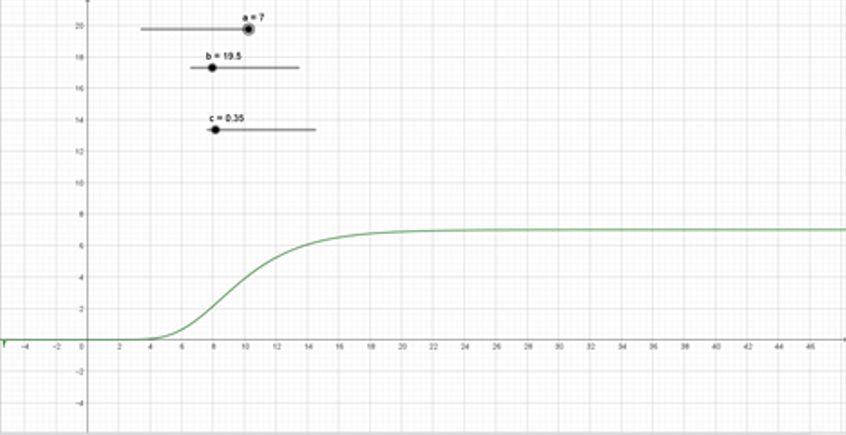
En l’anterior imatge, que és una simulació, la corba comença a disminuir el creixement a partir del dia 25, aproximadament, de l'inici de l'epidèmia i suposant que durant aquest període de temps hi ha un confinament de la població.
Si apliquem la corba de Gompertz a l'evolució de l'epidèmia a l'Estat espanyol durant el mes comprès entre el 25 de febrer i el 25 de març de l'any 2020 s'observa que el model s'ajusta perfectament a la realitat.
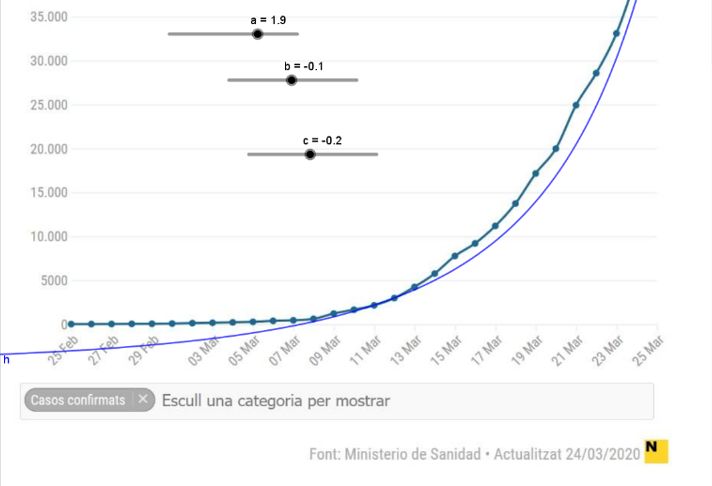
Les gràfiques de l'evolució del coronavirus a Catalunya i a Espanya proporcionades pel Ministeri de Salut.
Altres models més sofisticats requereixen coneixements d'equacions diferencials. Si es detecta una malaltia o plaga que pot immunitzar contra aquesta l'individu que l'ha patit, la idea és esbrinar l'evolució d’aquesta al llarg de diversos períodes (dies, mesos...), partint inicialment d'un nombre concret de persones infectades. És l'anomenat model SIR. En aquest model en la descripció de les variables es té en compte que, en cada etapa t, la població es divideix en tres grups:
S(t) els individus que són vulnerables, susceptibles de ser contagiats, I(t) els infectats i R(t) els immunes; si denotem N(t) a la població total s'estableix la igualtat:
N(t) = S(t) + I(t) + R(t)
A partir d'aquesta relació es realitzen anàlisis rigoroses amb epidemiòlegs, metges especialistes i matemàtics que condueixen a la resolució de sistemes d'equacions diferencials de la forma:
,
,
; sota certes condicions inicials, essent m i c paràmetres positius.
Per aprofundir en aquest tipus de model s’aconsella la lectura de l’article "Modelos matemáticos en un problema de epidemias", d'A. Vidal, F.J. Boigues, V.D. Estruch. Modelling in Science Education and Learning, Volume 9(2), (2016 )
Referències i fonts consultades
Alguns enllaços que poden ajudar a complementar i aprofundir la informació exposada:
1. https://www.covidvisualizer.com/ i https://cutt.ly/DtKSSR6 Es visualitza la propagació a escala mundial de la pandèmia en temps real.
2. https://www.washingtonpost.com/graphics/2020/world/corona-simulator/ Interessant estudi amb simulacions de la propagació de la covid-19.
3. https://covid19.isciii.es/ Informació actualitzada i diària, incloent-hi dades, de l'evolució de l'epidèmia a l'Estat espanyol. Pàgina oferta pel Ministeri de Ciència i Innovació.
4. https://catalunyaplural.cat/ca/5-grafics-actualitzats-per-seguir-levolucio-del-coronavirus-a-catalunya-espanya-i-el-mon/ Gràfics actualitzats de l'estat de la pandèmia en l'àmbit internacional.
5. https://web.gencat.cat/ca/coronavirus Pàgina oficial de la Generalitat de Catalunya amb les indicacions i últimes novetats en investigació i recerca. Inclou consells als ciutadans per al comportament en l'àmbit social.
6. https://cutt.ly/VtKDNxf i http://aquas.gencat.cat/ca/actualitat/ultimes-dades-coronavirus Mostra la situació actual de tots els municipis de Catalunya, amb xifres d'infectats i probabilitats de ser infectat. També la incidència d'infecció en cada territori.
7. https://gabgoh.github.io/COVID/index.html?CFR=0.0343&D_hospital_lag=5&D_incbation=5.2&D_infectious=2.9&D_recovery_mild=13 Sofisticada calculadora en línia de l'evolució d'una epidèmia. Es basa en el model SIR.





