Secrets i codis. Codis de la nostra vida: els codis de barres (VI)

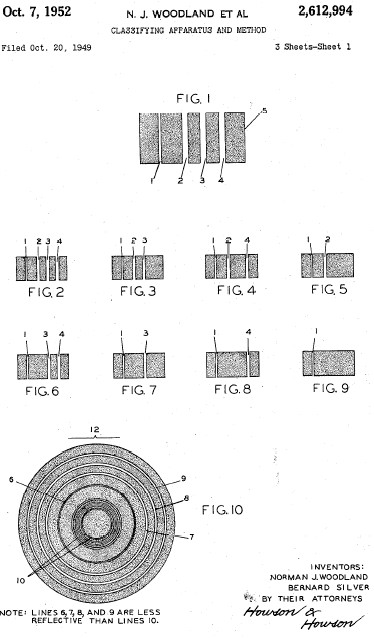El primer sistema de codis de barres va ser patentat el 7 d’octubre de 1952 per Norman Woodland i Bernard Silver, amb número de registre 2.612.994, encara que la patent es va sol·licitar l’any 1949.

Aquest primer codi de barres no s’assembla gens als que actualment coneixem perquè estava dissenyat mitjançant un seguit de cercles concèntrics. Tanmateix, al cap de vint anys, un comerç feu la primera lectura d’un codi de barres, que va tenir lloc l’any 1974 en un comerç de Troy, Ohio (EUA).

El format actual consisteix en una sèrie de barres negres (que en sistema binari representen l'1) i espais en blanc (que en binari representen el 0) de diferents amplades que estan incorporats en etiquetes de productes per tal d’identificar articles i de ser llegits amb dispositius electrònics.

Els codis de barres actualment els trobem gairebé a tot arreu, especialment en productes d’alimentació, objectes de regal, joguines, peces de vestir, etc., i ofereixen informació codificada sobre els productes (origen, composició, fabricant, etc.).

Hi ha diversos tipus de codis de barres: l'EAN en la seva versió de 13 dígits (EAN-13), l'EAN-8, l'UPC-12, etc. Tot seguit en mostrarem algun.

Codi EAN-13

L’acrònim EAN-13 prové d’European Article Number i va néixer als voltants de l’any 1976. Actualment està implantat a escala internacional i consta d’una trentena de barres codificades en 13 dígits (ABCDEFGHIJKLM).

La seva distribució i significat més usual és:

Malgrat que en alguns mitjans es parla d’un suposat codi de barres que identifica els productes catalans amb un 15 al començament, en lloc d’un 84, podem dir que això és fals perquè Catalunya no té codi identificador propi. Per això, aconsello la lectura d'aquest article de Vilaweb. 

El criteri per establir l’autenticitat d’un codi de barres és sumar tots els dígits que ocupen un lloc senar, més tres vegades la suma de tots els dígits que ocupen un lloc parell (això només amb els dotze primers), més el dígit de control, i el resultat ha de ser un múltiple de 10.

De manera equivalent: A + C + E + G + I + K + 3(B + D + F + H + J + L) + M = 0 (mòd. 10, és a dir, el resultat ha de ser múltiple de 10).

Ara, verificarem que el codi d’aquest envàs d’aigua és el correcte i que, per tant, no es tracta d’una falsificació.

Efectuem 8 + 1 + 8 + 1 + 0 + 0 + 3(4 + 3 + 7 + 0 + 3 + 4) + 9 = 90, que és múltiple de 10, per tant és correcte.

Cercant el número amagat!

En el paquet de cacau que mostrem apareix un dígit del codi de barres esborrat, cercarem quin és. Componem els dígits segons l’algoritme i anomenem X

al dígit desconegut: 

4 + 1 + 3 + 0 + 3 + 4 + 3(0 + 3 + 2 + 0 + X + 9) + 7 = 64 + 3 · X = múltiple de 10

 Notem que X ha de ser 2. Llavors el codi correcte és:

Codi EAN- 8

El codi EAN-8 està format per 8 dígits, ABCDEFGH, i s’utilitza en productes que, per diverses raons, no és possible assignar-los l'EAN-13.

S’estructura en tres parts: codi del país, codi del producte i dígit de control (H). L’algoritme de verificació és anàleg al de l'EAN-13.

Es considera la suma dels dígits que ocupen una posició parell amb el triple dels que ocupen una posició senar (excloent-hi el dígit de control), el resultat –diguem-li R– cal que sigui múltiple de 10. Aleshores s’estableix que el dígit de control H és H = 10 - R (si R és diferent de 0) i si R = 0 s’agafa com a dígit de control el 0.

Per exemple, si volem calcular si el dígit de control del codi EAN-8 codificat com a 84-15732-2 és correcte, fem: 3 · (8 + 1 + 7 + 2) + 4 + 5 + 3 + 2 v = 50, que és múltiple de 10. Per tant, podem dir que és correcte.

O un altre exemple. Si volem verificar que el dígit de control és efectivament el 8 en el cas del iogurt Danonino, un producte de consum habitual a moltes llars, i que té el codi de barres 84105028 (com podem veure a la imatge), llavors haurem de calcular: 

3(8 + 1 + 5 + 2) + 4 + 0 + 0 + 8 = 60, que és múltiple de 10. Una vegada més, podem concloure que és correcte.