Una història d’harmonia i de misteri

Música: la sèrie harmònica

La sèrie harmònica és una seqüència de sons —tons purs representats per ones sinusoidals— en què la freqüència de cada so és un múltiple enter de la freqüència més baixa de totes, una nota base anomenada fonamental.

Sèrie harmònica musical

Sovint, els instruments musicals contenen un ressonador acústic, sigui una corda o una columna d'aire, que oscil·la en nombrosos modes simultàniament. A la freqüència corresponent a cada mode vibrador, les ones viatgen en ambdues direccions al llarg de la corda o de la columna d'aire, reforçant-se i cancel·lant-se les unes amb les altres per formar ones estacionàries. La interacció amb l’aire circumdant provoca ones sonores audibles que es desplacen lluny de l’instrument. A causa del distanciament típic de les ressonàncies, les freqüències es limiten majoritàriament a múltiples enters, o harmònics, de la freqüència més baixa. Aquests múltiples constitueixen la sèrie harmònica.

El to musical d’una nota es percep normalment com el present parcial més baix (la freqüència fonamental), que es crea per vibracions a tota la longitud de la corda o columna d’aire, o com un harmònic superior escollit pel reproductor. I el timbre musical d'un to constant d'un instrument així està fortament afectat per la força relativa de cada harmònic. Component harmònics adequadament es poden construir músiques sublims i experimentar un plaer indescriptible, inigualable, un dels més grans que ens és donat de gaudir amb els nostres sentits.

La sèrie harmònica en matemàtiques

No té, doncs, res d’estrany que, en matemàtiques, la sèrie harmònica es defineixi així:

1 + 1/2 + 1/3 + 1/4 + ...

Correspon a la suma de totes les longituds d’ona de les notes successives de la corda vibrant, que són, com ja hem dit, 1/2, 1/3, 1/4, etc., de la longitud d’ona fonamental. Cada terme de la sèrie posterior al primer és la mitjana harmònica dels seus termes veïns.

La sèrie harmònica està molt lligada a la funció més important i misteriosa de tota la matemàtica: la funció dseta ζ (en anglès coneguda com a zeta function ζ; i aquesta és també la nomenclatura que s’usa normalment en català i castellà: funció zeta, i que faré servir aquí).

Paradoxes de l’infinit

Però parlem primer de sèries en general. Una sèrie matemàtica és una suma infinita, és a dir, que consta d’infinits termes. Ja a la Grècia clàssica els filòsofs tenien molts problemes amb el concepte d’infinit. Qui no recorda les famoses paradoxes de Zenó d’Elea, deixeble de Parmènides i que en va escriure tot un llibre per tal de defensar la filosofia del seu mestre. Malauradament el llibre es va perdre fa molts segles i tot el que ara en sabem prové d’Aristòtil i de Simplici; sobretot d’aquest darrer, que encara que escrigué mil anys després que Zenó sí que encara posseïa el seu llibre. A la Stanford Encyclopedia of Philosophy hi ha una descripció molt acurada de totes aquestes paradoxes [https://plato.stanford.edu/entries/paradox-zeno/].

Aquí em fixaré només en dues. Una és la que afirma que el moviment resulta impossible. Si un arquer dispara una fletxa, abans que aquesta arribi al blanc haurà primer de recórrer la meitat de la distància fins a aquest. I, encara abans, haurà d’arribar a la meitat de la meitat de la distància. I, abans, a la meitat de la meitat de la meitat; i així successivament. Podríem estar repetint aquest argument hores i hores, i la conclusió és que la fletxa no pot ni sortir de l’arc de l’arquer. I això ho podríem aplicar a qualsevol altre moviment. Tot moviment és impossible.

L’altra paradoxa és la tan coneguda d’Aquil·les i la tortuga. Per molt que Aquil·les corri per tal d’atrapar la tortuga no ho podrà fer mai, i molt menys avançar-la. En efecte, quan Aquil·les arribi al lloc en què es troba ara la tortuga, aquesta ja no hi serà, s’haurà desplaçat de la seva posició; i quan arribi a la nova posició la tortuga ja serà més enllà, i així successivament. Podem repetir l’argument de manera indefinida, anys i anys sense acabar mai. De fet, considerant-ho com una argumentació filosòfica, en cada pas de l’argument estaríem exactament en la mateixa situació inicial: res ens impedeix posar-hi una lent òptica d’augment i podríem fer que la distància romanent fos sempre ben bé la mateixa que al principi. Això contradiu del tot l’experiència quotidiana, d’aquí que rebi el nom de paradoxa.

L’intent de resoldre aquestes paradoxes ens porta de cap a les sèries matemàtiques, de les quals he parlat abans. Resoldré la segona, la primera la deixo com a petit exercici per al lector o lectora. Simplificant, si suposem que Aquil·les va el doble de ràpid que la tortuga, quan Aquil·les arribi a la posició inicial d’aquesta, la tortuga ja no serà allí doncs haurà recorregut una meitat de la distància inicial; quan Aquil·les arribi a la nova posició, la tortuga haurà fet ara una quarta part de la distància inicial, i així successivament. Si a la distància inicial li diem 1, la suma de les distàncies successives recorregudes per Aquil·les és una sèrie infinita:

1 + 1/2 + 1/4 + 1/8 + 1/16 + ...

I és que aquí hem portat la paradoxa filosòfica al terreny de la física i la matemàtica. La lupa de què he parlat abans, i que ens deia que a cada pas de l’argument ens trobàvem exactament en la mateixa situació inicial, ara ja no té sentit, perquè hem introduït les magnituds d’espai i temps, amb unitats de mesura. Comptant els espais recorreguts i el temps emprat a cada un, arribem en ambdós casos a la mateixa sèrie matemàtica; que encara que té un nombre infinit de termes dona un resultat finit i ben senzill: 2. En altres paraules, Aquil·les arribarà exactament a atrapar la tortuga quan aquesta s’hagi allunyat la mateixa distància que els separava inicialment; i pel que fa al temps, quan hagi passat el doble del temps que Aquil·les va emprar per arribar a la posició inicial de la tortuga. Però, com sabem que la suma d’aquesta sèrie d’infinits termes val exactament 2? Molt senzill. Posem de moment que val x. És ben clar que hom pot escriure:

1 + 1/2 + 1/4 + 1/8 + 1/16 + ... = 1 + 1/2 (1 + 1/2 + 1/4 + 1/8 + 1/16 + ... )

x  =  1 + ½ x    i d’aquí   2 x  =  2 + x,   d’on   x = 2.

Abans de passar a qüestions més difícils, posaré un altre exemple senzill però que va fer que molta gent s'hi capfiqués. La sèrie alternada:

1 - 1 + 1 - 1 + 1 - 1 + 1 - ...

Té també un indubtable misteri: segons on ens quedem en sumar, la suma val 0, i segons com, sembla que val 1. El nombre infinit de termes, serà parell o bé senar? Actuem com abans, no sabem el que val aquesta suma, diguem que val x, i podem ara agrupar, convenientment:

1 - 1 + 1 -1 + 1 - 1 + 1 - ... = 1 - (1 - 1 + 1 - 1 + 1 -...),

o sigui:  

x = 1 – x,

d’on 

2 x = 1,    x = 1/2,

un valor raonablement democràtic i que també s’obté per mitjans matemàticament rigorosos, que seran els que descriuré a partir d’ara.

La funció zeta

El gran Leonhard Euler va dedicar grans esforços a estudiar les sèries infinites. La sèrie harmònica el fascinava i es va adonar que posant un petit exponent al nombre natural que correspon a la freqüència

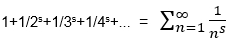
obtenia per a la suma dels infinits termes resultats espectaculars, com ara els següents. Quan l’exponent s era 2,

π² / 6,

i quan l’exponent s era 4, 6, 8,

π⁴ / 90,   π⁶ / 945,   π⁸ / 9450,

respectivament. Encara més, Euler va obtenir tots els resultats fins a la potència 26. De fet, hi ha una expressió tancada per a qualsevol exponent parell, en termes de πⁿ i els coneguts com a nombres de Bernoulli.

Però, quan l’exponent és 1, estem en el cas inicial de la sèrie harmònica, i no hi ha manera humana d’obtenir un valor finit. No podem evitar el fet que la suma d’aquesta sèrie sigui logarítmicament divergent vers l’infinit. Sent més precisos, si sumem un nombre N de termes de la sèrie, el valor de la suma es comporta com el Log N. Euler va derivar importants propietats d’aquesta sèrie com a funció de s, no només per a valors parells o naturals de s, sinó també per a altres valors reals de la variable. Un dels més importants és la relació d'aquesta funció amb els nombres primers: la funció zeta és igual a un producte infinit estès a tots els nombres primers, p,

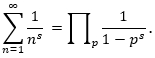
Però va ser Bernhard Riemann qui va anar molt més enllà i descobrí la importància extraordinària d’aquesta funció quan es permet que s sigui un número complex. Va definir la funció zeta, ζ(s) –avui anomenada funció zeta de Riemann– de la manera següent:

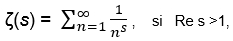
és a dir, quan la part real de la variable s és més gran que 1 (llavors la sèrie és absolutament convergent, es pot sumar sense cap problema i dona un resultat finit). I què passa per a la resta de valors de s que no satisfan aquesta condició? Riemann va demostrar que aquesta sèrie es pot estendre de manera única a tota la resta del pla complex, C. A tots els seus punts dona un valor finit, amb una única excepció, que és quan s = 1, en què recuperem la sèrie harmònica, que és inevitablement divergent. Aquest esdevé, doncs, l’únic punt singular de la funció zeta, en tot el pla complex.

Per altra banda, la recta del pla complex Re s  = 1/2  (paral·lela a l’eix d’ordenades) gaudeix d’una importància excepcional. En concret, la conjectura de Riemann (o hipòtesi de Riemann, considerada per molts el problema matemàtic més important sense resoldre de la història) afirma que els punts del pla complex on la funció zeta val zero es troben tots situats en aquesta línia (a part, és clar, dels zeros trivials, ben coneguts, que s’obtenen quan s = - 2n, on n és un nombre natural arbitrari).

La funció zeta és una funció meravellosa i alhora carregada de misteri. Molts la consideren la funció més important de tota la matemàtica. La podem veure com si fos un oracle, o una profetessa, ara explicaré el perquè. Jo mateix li he dedicat una part important de la meva vida, n’he estudiat alguns aspectes [1,2,3], i sobre els meus descobriments he fet conferències en un bon grapat de les millors universitats del món [4].

En poques paraules, mitjançant la funció zeta, sèries infinites terriblement divergents poden ser conduïdes a donar valors finits, i ben petits. I el que és més important, aquests valors, que molts cops semblen absurds, d’entrada, adquireixen al final un sentit ple, sent del tot validats pels experiments de laboratori més extraordinàriament precisos que s’hagin dut a terme mai.

La doma dels infinits

El que ara ve pot semblar pura màgia, però és d’un rigor matemàtic absolut. Preguntem-nos, per començar, quant val la suma

1 + 1 + 1 + 1 + 1 + ... ?

Una primera resposta seria: infinit. Es tracta, sens dubte, de la definició més senzilla que hom pot donar de l’infinit. Això és correcte, però no gaire útil. Resulta que les sèries més importants que apareixen en les teories més avançades de la física, les teories de camps quàntics, com ja es va veure en els anys 30 del segle passat, són totes divergents i una resposta així en res ajuda a donar-los-hi sentit. Surten infinits a dojo! Una altra resposta molt més adequada seria: val -1/2.

En més d'una ocasió he pres part en seminaris (en recordo ara dos, un de Francisco Ynduráin, de la Universitat Complutense de Madrid, i un altre d'Andrei Slavnov, de l'Institut de Matemàtiques Steklov de Moscou) en què el ponent ha dit en algun moment durant la seva exposició aquesta frase (o una de molt semblant):

"As everybody knows, 1 + 1 + 1 + ... = -1/2."

Amb això donà per fet que tots els presents coneixien ja el valor d'aquesta suma. Recordem el lema que hi havia escrit sobre la porta d'entrada de l’Acadèmia de Plató: No entri aquí qui no sàpiga geometria. Aquests il·lustres conferenciants venien a dir el mateix: qui no sàpiga quant val aquesta suma ja se’n pot anar perquè no entendrà res. N’hi ha que van encara més enllà i classifiquen les persones en dos grups: el de les que no saben això i el de les que sí que coneixen aquest secret insondable.

Però, com s'arriba a un valor tal, en aparença absurd i antiintuïtiu? I quin sentit o utilitat pot tenir de fet, a la pràctica?

Cada pocs anys aquesta història reapareix amb molta força, de bell nou. Ara es compleixen sis anys de la darrera vegada en què va adquirir gran popularitat gràcies a un vídeo del periodista Brady Haran i els físics de la Universitat de Nottingham Ed Copeland i Toni Padilla. El vídeo [https://youtu.be/w-I6XTVZXww] es titula (tradueixo):

SORPRENENT: 1 + 2 + 3 + 4 + 5 + ... = -1/12

I tingué un milió i mig de visites en pocs dies (avui ja n’acumula set i mig). El New York Times se’n va fer ressò amb un article de Dennis Overbye (4 feb. 2014, p. D6, [https://www.nytimes.com/2014/02/04/science/in-the-end-it-all-adds-up-to.html]). Ben cert, aquest resultat sembla encara més espectacular que el que he esmentat abans, però s’explica exactament de la mateixa manera, com ara veurem.

Si un s’ho mira a fons, veurà que el secret s’amaga en les extraordinàries propietats del camp complex. Si algú no sap que és això, a les lliçons de "Física per a idiotes" [http://physicsforidiots.com/maths/complex-numbers/] s'hi troba una magnífica introducció d’aquest concepte, acabada amb la fórmula més sorprenent de tota la matemàtica:

e^iπ + 1 = 0

Per molt que m’estengués em seria impossible donar tan sols una lleugera idea de la importància excepcional que tenen els números complexos a la física. Sense ells cap teoria no seria possible. Tot i que no són nombres reals i, en conseqüència, el resultat de la mesura d’una magnitud de la natura no vindrà mai expressat sota la forma d’un número complex. Ja hem vist que en la definició de Riemann de la funció zeta tenen un paper cabdal, permetent definir aquesta funció d’una manera unívoca (sense ambigüitat) i finita (excepte en el punt s = 1).

Doncs, dit i fet. Comencem per la sèrie que sembla més senzilla:

1 + 1 + 1 + 1 + 1 + ...

i acudim al nostre oracle, la funció zeta. Aquesta expressió l'obtenim a partir de ζ(s) quan la potència s val 0:

ζ(0).

Prenem, doncs, la funció zeta de Riemann, definida sobre tot el pla complex, i vegem quin valor dona quan s = 0. Aquest valor és -1/2. Ja hem acabat.

Fem ara el mateix amb l’altra sèrie:

1 + 2 + 3 + 4 + 5 + ... 

Aquesta correspon a la funció zeta, quan hi posem s = -1:

ζ(-1).

Però, quant val la funció zeta de Riemann en aquest punt del pla complex s = -1? Doncs val -1/12. I podríem continuar així amb tantes i tantes altres sèries divergents. Però malauradament se’ns ha acabat el temps.

La funció zeta ens dona un mètode per a sumar sèries divergents d’una manera unívoca i ben definida. Es tracta d’una eina poderosíssima i és per això que, en emprar-la, un pot fer-se mal molt fàcilment. El nombre d’equivocacions greus aparegudes a la literatura científica, com a resultat d'haver aplicat el mètode erròniament, és de fet extensíssim. Són bastants també els autors que han arribat a afirmar, decebuts, que aquest procediment no funcionava, quan de fet s’ha demostrat sempre que eren ells els qui cometien errades imperdonables (fins i tot infantils) en l'us que en feien del mètode. Vegem-ne un petit exemple, de mala praxi. La sèrie següent, per molt que senzilla, és fonamental en física quàntica; correspon a les fluctuacions del buit quàntic per al model d’oscil·lador harmònic (ometo, per simplificar, les constants fonamentals que hi intervenen i tota la meravellosa física que hi ha al darrere [3]):

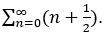
Un error comú, que podria cometre algú que es pensés que amb el que he explicat ja s’ha fet tot un expert en aquests càlculs (això passa molt sovint!), seria separar-ho en dues sèries  (el ½ addicional correspon a n = 0):

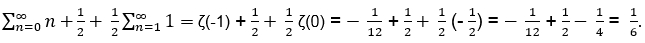
Aquest resultat és erroni. El mètode s’ha d’aplicar per als valors espectrals d’entrada (entre parèntesis) i el resultat correcte s’obté fent servir una altra funció zeta, la de Hurwitz:

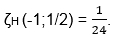
Per aclarir aquest punt es poden consultar les meves referències [5,1,2,3].

Però la pregunta clau és, sens dubte, si aquests valors estranys, del tot incomprensibles, que hem obtingut de manera matemàtica, tenen o no a veure amb la realitat física, amb el comportament de la natura. La resposta és, òbviament, que sí, i del tot! De fet ja l’he donat abans, encara que de manera indirecta: si grans físics com Slavnov i Ynduráin (entre molts d’altres) han basat les seves teories en aquest mètode és perquè els resultats són igualment excepcionals. S’ajusten als valors dels resultats experimentals dels grans laboratoris de la física d’altes energies (CERN, DESY, SLAC, KEK, etc.) amb quinze xifres decimals, pel cap baix, una rere l’altra.

Un fet així tenim dret a considerar-lo misteriós: és el gran misteri que dona títol al present blog.

_____________________________________________

[1] E. Elizalde, Ten Physical Applications of Spectral Zeta Functions, Springer 2012, 2nd Ed.  https://www.springer.com/gp/book/9783642294044

[2] E. Elizalde et al., Zeta Regularization Techniques with Applications, World Scientific,  1994.   https://books.google.es/books/about/Zeta_regularization_techniques_with_appl.html?id=PXkhYSqIeykC&redir_esc=y&hl=en

[3] E. Elizalde, "El efecto Casimir", Investigación y Ciencia, març 2009.    https://www.investigacionyciencia.es/revistas/investigacion-y-ciencia/enclado-478/el-efecto-casimir-1285     

[4] E. Elizalde, Phillips Auditorium, Harvard University, Cambridge, EUA.    http://cfa-www.harvard.edu/dvlwrap/itamp/0211/elizalde.ram   

[5] E. Elizalde, "Zeta-Function Regularization is Uniquely Defined and Well", Journal of Physics A 27 (1993) 1.  https://www.researchgate.net/publication/2072281_Zeta-Function_Regularization_is_Uniquely_Defined_and_Well